Statistica

L'analisi di dati funzionali è l'analisi statistica di campioni di funzioni di una o più variabili continue (tempo, spazio, frequenza). I dati sono realizzazioni di variabili casuali a valori in spazi infinito-dimensionali, che vengono però osservati in corrispondenza di un insieme finito di punti del dominio. La ricerca in questo ambito si occupa di ricostruire le funzioni (smoothing, allineamento) e fare inferenza sulle funzioni ricostruite (stima di parametri, confronto tra gruppi, regressione, previsione di una nuova curva, ...).
Parole chiave e temi trattati:
Inferenza locale, inferenza globale, multiple testing, regressione, allineamento, smoothing bayesiano.
Persone coinvolte:
L’analisi sequenziale è un ramo della statistica inferenziale in cui il numero delle osservazioni non è fissato in anticipo. Formalmente inizia negli anni ’40, quando Abrahm Wald introduce il “sequential probability ratio test”, una procedura per testare due ipotesi statistiche basata sull’osservazione sequenziale di dati sino a quando non vi è evidenza in favore di una delle due ipotesi. La linee principali di ricerca sono: (1) costruzione di test sequenziali per diversi tipi di processi stocastici e per un numero di ipotesi superiore a due; (2) analisi di problemi di “change-point detection”, dove un processo con certe caratteristiche statistiche iniziali viene monitorato sequenzialmente, eventualmente anche entro un periodo di tempo prestabilito, per identificare il momento in cui tali caratteristiche si modificano.
Parole chiave e temi trattati:
Arresto ottimale (optimal stopping); test sequenziali (sequential testing); problemi di rilevazione del punto di cambiamento o del disordine (change-point detection or disorder problems); rilevazione di frodi (fraud detection); moto Browniano e processi di Lévy (Brownian motion and Lévy processes); strategie di trading (trading strategies); problemi a frontiera libera (free-boundary problems); metodi numerici per problemi sequenziali (numerical methods for sequential problems).
Persone coinvolte:
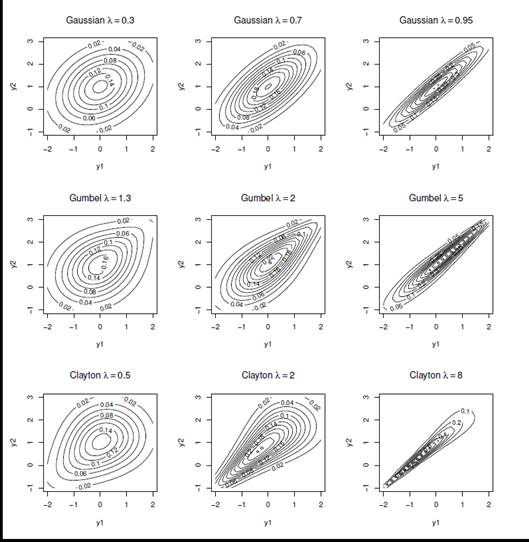
In statistica la copula costituisce un utile strumento che consente di modellare facilmente la dipendenza o associazione fra due o più variabili nella costruzione di distribuzioni multivariate. Copule diverse inducono diverse tipologie di dipendenza, dalla copula Gaussiana che descrive un legame lineare fra le variabili a copule più complesse come le copule dei valori estremi che descrivono associazioni nelle code delle distribuzioni.
In presenza di due o più variabili di risposta categoriali, binarie o rilevate su scala ordinale le copule costituiscono un utile strumento per modellare la dipendenza fra le probabilità di risposta al fine di costruire modelli per la stima congiunta del rischio di accadimento di eventi complessi, spesso rari e dipendenti fra loro.
Questi modelli possono essere impiegati in diversi ambiti: nello studio del rischio di credito per la stima delle insolvenze, nello studio del rischio sistemico e per la misurazione del rischio cibernetico, ma anche in ambito clinico nello studio congiunto di efficacia e tossicità di un farmaco.
Parole chiave:
Copula, eventi rari, eventi estremi, modelli per variabili ordinali, variabili di risposta binarie, dipendenza, associazione, risk model and Cyber risk, Modelli vine copula.
Persone coinvolte:
Rosario Barone, Silvia Facchinetti, Silvia Osmetti

Il disegno ottimo degli esperimenti è una disciplina che si occupa di pianificare la raccolta dei dati in modo tale da massimizzare la qualità delle informazioni ottenute, minimizzando al contempo il costo, il tempo e le risorse necessarie. Il suo obiettivo principale è scegliere le condizioni sperimentali, vale a dire i valori dei fattori indipendenti, in modo da ottimizzare la precisione delle stime dei parametri del modello o l'efficacia delle capacità predittiva del modello. In generale la ricerca sul disegno degli esperimenti – sviluppata sia in ambito frequentista che bayesiano - si occupa di individuare le dimensioni campionarie e le condizioni sperimentali ottimali (sia in fase di disegno di screening che di disegno follow-up) per gli obiettivi di ricerca come, ad esempio, la discriminazione tra modelli. Gli ambiti di applicazione variano dalle sperimentazioni scientifiche, alla ottimizzazione di processi industriali, agli studi clinici e di replicazione. Recentemente si è verificato come la adozione della teoria del disegno ottimo degli esperimenti sia particolarmente efficace per estrarre le informazioni più rilevanti da un Big Dataset. Questa caratteristica risulta di interesse nel machine learning per l'apprendimento supervisionato con vincoli di misurazione (vale a dire la circostanza per la quale è semplice ed economico ricavare le informazioni sui predittori, mentre le risposte sono indisponibili e costose da ottenere).
Parole chiave e temi trattati:
D-ottimalità, A-ottimalità, I-ottimalità, ampiezza campionaria, studi di replicazione, riduzione dei dati, selezione del modello, modelli a scelta discreta, copula, disegni individualizzati.
Persone coinvolte:
Federico Castelletti, Guido Consonni, Laura Deldossi, Silvia Osmetti

La ricerca in questo campo si occupa di sviluppare metodi statistici per la scelta del miglior modello statistico all’interno di una prefissata classe di modelli, per la descrizione dei dati e delle relazioni tra variabili. Con l’avvento dei Big Data e la grande disponibilità di variabili che possono descrivere un fenomeno, si pone il problema di trovare metodi efficaci per la selezione di quelle più importanti.
Parole chiave e temi trattati:
Bayes Factor; Metodi computazionali; Metodi bayesiani oggettivi; Modelli vincolati; Modelli di regressione con g-priors; Metodi computazionali di selezione delle variabili; Regressioni Lasso.
Persone coinvolte:
Rosario Barone, Roberta Paroli

I metodi di clustering basati sulla densità o sul modello (density-based/model-based clustering) rappresentano strumenti avanzati per l’identificazione di raggruppamenti nei dati. Questi metodi si basano sui modelli mistura, che costituiscono il framework probabilistico naturale per la modellizzazione di popolazioni eterogenee. La stima dei parametri viene effettuata mediante approcci statistici rigorosi: da un lato, mediante la massimizzazione della verosimiglianza nel contesto frequentista; dall’altro, tramite l’identificazione della distribuzione a posteriori nel contesto Bayesiano. Questi approcci non solo garantiscono una allocazione interpretabile, ma permettono anche di quantificarne l’incertezza. La ricerca si propone di sviluppare estensioni metodologiche per il density-based clustering in scenari complessi, come quelli che coinvolgono dati contaminati o ad alta dimensionalità, nonché in contesti dinamici e temporali.
Parole chiave e temi trattati:
Model-based clustering, Bayesian clustering, Finite mixture models, Markov chain Monte Carlo, EM algorithm, Outliers detection, Robust estimation, Dynamic clustering, Random partition models.
Persone coinvolte:
Rosario Barone, Andrea Cappozzo, Federico Castelletti, Lucia Paci

I modelli grafici basati su networks vengono utilizzati in ambito statistico per stimare relazioni causali tra variabili a partire dalle osservazioni. Tipicamente il network generatore dei dati è incognito e si richiede una sua stima attraverso un processo inferenziale noto come "structure learning". La ricerca si propone di sviluppare metodologie bayesiane per l'apprendimento di modelli grafici e l'inferenza causale in contesti che includono: i) dati osservazionali; ii) dati sperimentali caratterizzati da gruppi di individui sottoposti a diversi trattamenti; iii) dati eterogenei caratterizzati da strutture di clustering latenti. Le metodologie sviluppate trovano impiego in ambito medico, sia clinico che genomico, e psicologico, particolarmente in studi di tipo psicopatologico.
Parole chiave e temi trattati:
Bayesian inference; causal effect; directed graph; network psychometrics; structure learning.
Persone Coinvolte:
Federico Castelletti, Guido Consonni, Lucia Paci, Stefano Peluso
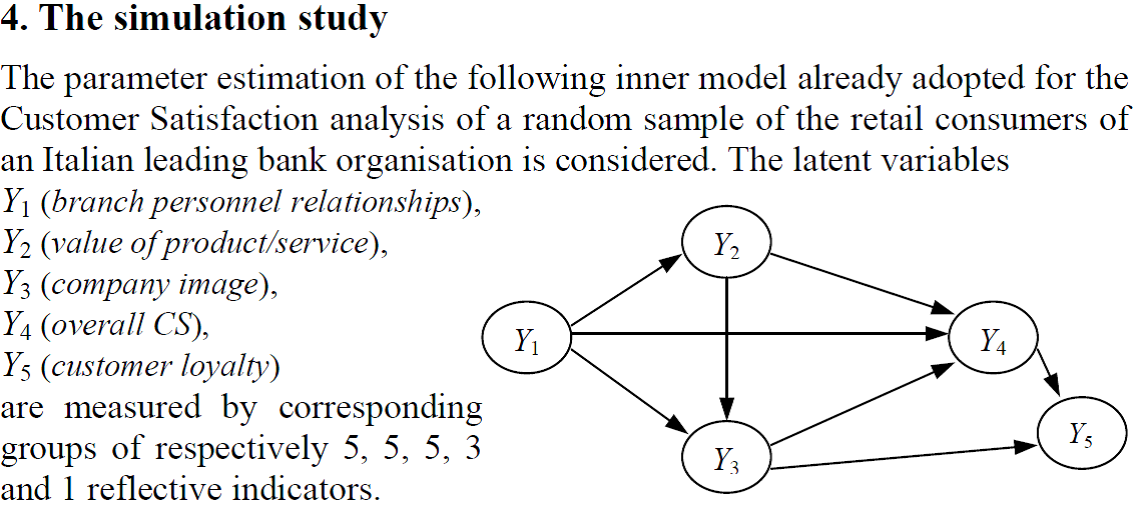
Implementazione efficiente dell’algoritmo PLS. Estensione dell’algoritmo in presenza di variabili ordinali. Definizione di un metodo di previsione in presenza di vairabili ordinali.
Parole chiave e temi trattati:
Partial Least Squares; Prediction; Structural equation models
Persone coinvolte:
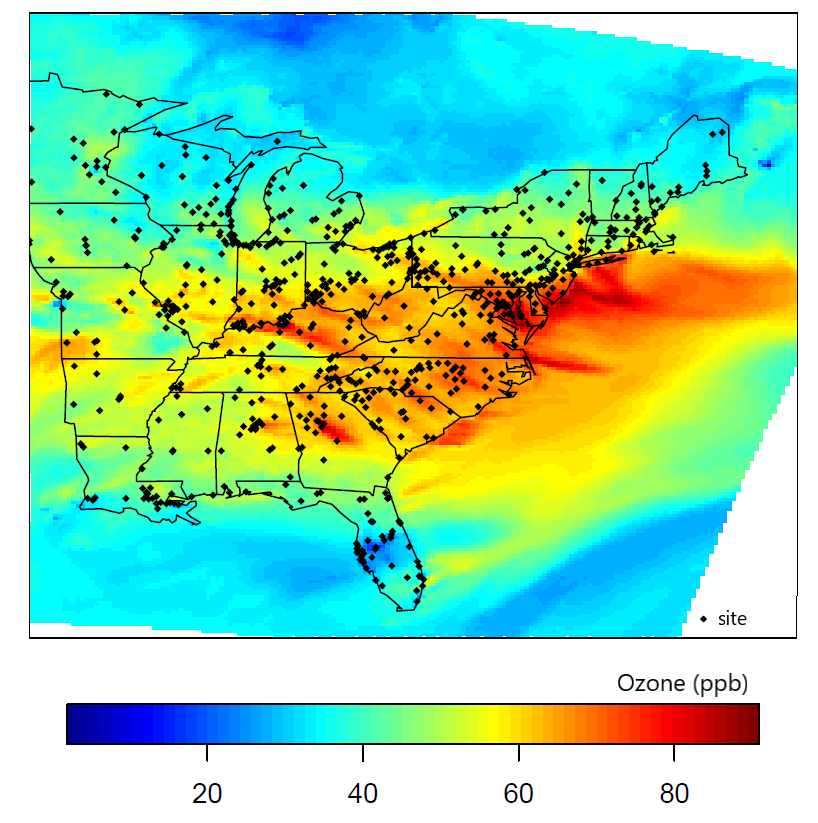
L'analisi delle serie temporali/spaziali è costituita da un insieme di metodi statistici atti a indagare l’evoluzione di una serie di dati che varia nel tempo o nello spazio.
Le applicazioni sono vastissime in tutti i campi del mondo reale: economia, finanza, scienze ambientali, ecologia, biologia, epidemiologia, medicina, neuroscienze.
L’analisi delle serie temporali riguarda dati raccolti in un dominio temporale, mentre l’analisi dei dati spaziali riguarda l’analisi statistica di dati raccolti in un dominio spaziale, come ad esempio lo spazio geografico.
La ricerca in questo campo si occupa di sviluppare modelli stocastici per l’inferenza sulla struttura di dipendenza temporale o spaziale e la previsione di variabili di interesse per istanti temporali futuri o in regioni del dominio spaziale dove i dati non sono stati osservati. Altro obiettivo è quello di risolvere i problemi metodologici che nascono in fase di stima dei modelli e nei test delle ipotesi anche in relazione alla crescente disponibilità di vaste quantità di dati legata alla diffusione di Big Data ed ai connessi problemi computazionali.
Parole chiave e temi trattati:
Econometria spaziale, Geostatistica, Modelli nonstazionari, Modelli spazio-temporali, Processi di punto; Hidden Markov Models: Modelli di mistura; Markov switching models; Modelli spaziali autoregressivi, Modelli di panel spazio-temporali, Modelli spaziali a scelta discreta, Modelli di microeconometria spaziale; Misure robuste di correlazione spaziale, Campionamento di dati spaziali, Steaming di dati spaziali, Analisi dei dati di immagini, Analisi dell’inquinamento di aria e acqua; Effetti degli errori di localizzazione e del geomasking, Applicazioni alla diffusione del Sar-Cov-2, Punti di cambiamento.
Persone Coinvolte:
Giuseppe Arbia, Rosario Barone, Lucia Paci, Roberta Paroli, Stefano Peluso
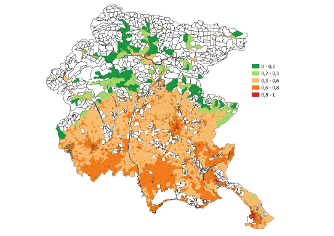
Last decades have seen increasing consensus towards the issue of climate change and rising awareness of the implied responsibility of human activity. With growing global warming, extreme climate events like heat waves have increased in duration, frequency and intensity leading to higher heat-related morbidity and mortality rates. In this context, heat vulnerability assessments play an important role supporting decision-makers in implementing targeted mitigation and prevention actions. With this motivation, this research aims to develop a heat vulnerability index by means of the Composite Indicator techniques to depict heat vulnerability of different geographical areas. In particular the propsed index is used to map heat vulnerability in the Friuli Venezia Giulia region at the census tract level. The results show that heat vulnerability follows a spatial pattern, where most vulnerable census tracts are located in urbanised and densely populated areas, lower risk is observed in rural areas and lowest danger in mountainous areas. The Performance Interval approach confirms that these results do not depend on the aggregation method used to construct the index.
Parole chiave o temi trattati:
Climate change, Heat waves, Composite indicator, Heat vulnerability index
Persone coinvolte: