Il clustering è una tecnica fondamentale per raggruppare una collezione di elementi/unità in base alle loro caratteristiche in modo tale da ottenere dei gruppi, chiamati cluster, che siano omogenei al loro interno e ben separati da ciascun altro gruppo, come nella nota euristica K-Means. Questa ricerca si concentra sullo studio teorico e algoritmico di problemi di clustering con vincoli di cardinalità, in cui ogni cluster deve contenere un numero di elementi ben stabilito. Lo studio analizza la complessità computazionale e gli algoritmi per varianti del problema con diverse metriche L_p in spazi a bassa dimensione e con rilassamento dei vincoli.

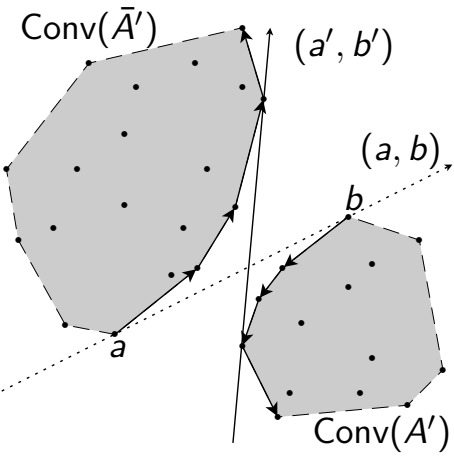
Dalle analisi iniziali emergono proprietà di separazione geometrica e condizioni di scambio tra cluster che caratterizzano le soluzioni ottimali. I problemi esaminati risultano computazionalmente difficili in molte configurazioni parametriche, anche in caso di bipartizione in dimensione uno. Ciononostante gli studi hanno prodotto algoritmi esatti efficienti, anche mediante programmazione dinamica, per certe sottoclassi di problemi, sfruttando strumenti di geometria combinatoria e algebrica come k-set e CAD, oltre a strutture dati dinamiche, quali alberi bilanciati adattati.

Questi risultati contribuiscono allo studio del clustering bilanciato, evidenziando limiti computazionali e fornendo soluzioni ottimali, con ricadute su applicazioni in diversi ambiti, come il bilanciamento del carico, la segmentazione di mercato, la compressione dei dati e l'allocazione equilibrata di risorse.

Parole chiave e temi trattati:

Clustering vincolato, Vincoli di cardinalità, Complessità computazionale, Algoritmi esatti, Norma Euclidea, Norma di Manhattan, k-set, Ottimizzazione discreta, Algoritmi polinomiali

Persone coinvolte:

Jianyi Lin