Meccanica dei mezzi continui e applicazioni

(Alfredo Marzocchi - Alessandro Musesti - Giulia Giantesio - Carlo Banfi)

Equazioni di bilancio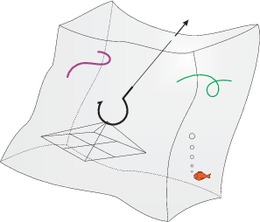

Questo filone di ricerca riguarda la generalizzazione e la sistemazione dei fondamenti della Meccanica dei continui, con un duplice obbiettivo:

1) l’assiomatizzazione e la solidità matematica delle argomentazioni classiche della Meccanica dei continui, nello spirito di quella che C. A. Truesdell definiva “Rational Continuum Mechanics”;

2) la possibilità di inquadrare in una cornice teorica unificata i modelli più recenti di materiali speciali, che ammettono singolarità quali sforzi o flussi concentrati, in modo da gettar luce su proprietà generali delle soluzioni di molti problemi di natura applicativa.

In particolare, il gruppo di ricerca studia i materiali di gradiente più elevato in un contesto di Potenze Virtuali generalizzate, basato su di un approccio geometrico ai sistemi dinamici di dimensione infinita. Un esempio esplicito è quello dei fluidi lineari isotropi di secondo gradiente, che ben si prestano a modellizzare interazioni non standard come l'aderenza tra tra fluido e strutture unidimensionali e altre interazioni concentrate.

Problemi di superfici minime di tipo Kirchhoff-Plateau e applicazioni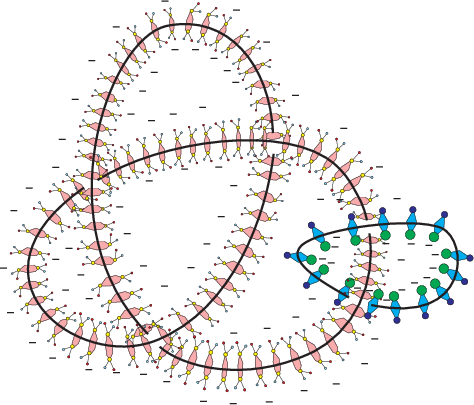

In questa ricerca si studiano problemi di minimo dell'energia elastica di una barra chiusa che circonda una superficie che deve minimizzare la sua area. Problemi di questo tipo sono delle generalizzazioni del classico problema di Plateau, nel quale la superficie di area minima deve contornare una curva data, anche irregolare. In questi problemi si tiene conto sia dell'effetto elastico del bordo sia del suo spessore, e questi può formare un nodo di dato tipo e addirittura un link tra diverse barre. Uno dei punti di maggior interesse è il modo in cui la superficie si appoggia alla barra, per il quale esistono caratterizzazioni topologiche. Simili strutture, nelle quali la trazione esercitata dalla pellicola è comparabile con le forze elastiche in gioco nel bordo, si osservano a livello microscopico.

Lago di Garda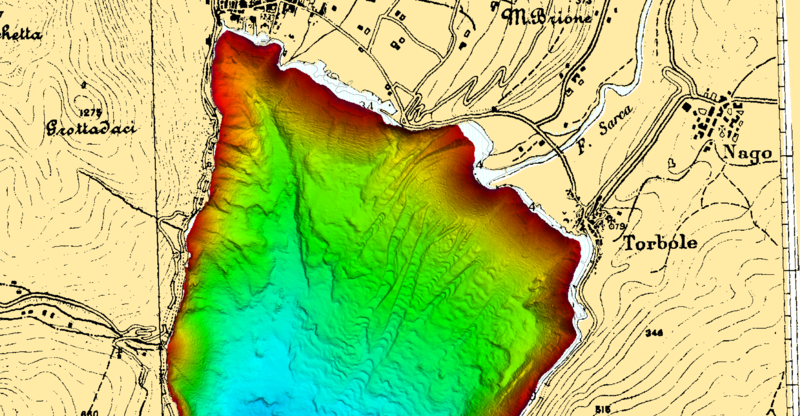

La ricerca fa parte del più ampio progetto strategico di Ateneo ACCURATE e si prefigge di creare una modellizzazione completa e accurata del moto delle acque in risposta agli agenti esterni e di situazioni estreme del bacino del Garda. Il modello terrà conto dei contributi del vento, della temperatura e dell'immissione di acque sia naturali che eccezionali. Allo stato attuale si sta procedendo alla scansione del fondo ad alta risoluzione mediante uno scanner multibeam in collaborazione con l'Istituto Idrografico della Marina, che ha prodotto l'immagine visualizzata.

Modellizzazione del muscolo scheletrico

Un altro ambito di ricerca è la modellizzazione matematica del muscolo scheletrico, anche in vista di un'applicazione allo studio di patologie quali la sarcopenia. Tale sindrome infatti, pur essendo oggetto di numerosissimi studi, è usualmente trattata soltanto dal punto di vista clinico e da quello statistico. L’obiettivo principale di questo ambito di ricerca è invece quello di fornire uno strumento alternativo, di tipo quantitativo, mediante la predisposizione di un modello matematico ad hoc che possa anche essere implementato al calcolatore, fornendo delle simulazioni realistiche. La costruzione di tale modello, partendo da un’energia iperelastica per un materiale trasversalmente isotropo, vuole tenere conto delle principali caratteristiche del muscolo scheletrico: incomprimibilità, non linearità, anisotropia, attivazione.

Soluzioni esatte in fluidodinamica per diverse classi di fluidi

Un altro ambito di ricerca è quello che riguarda lo studio di soluzioni esatte in fluidodinamica. Tali soluzioni, esplicite o numeriche, descrivono alcune situazioni reali (sufficientemente semplici dal punto di vista geometrico o delle condizioni al contorno) in cui un fluido risponde all'ambiente circostante (come ad esempio il moto in un canale o il moto con un punto di ristagno in cui il fluido colpisce un oggetto). Spesso queste situazioni hanno importanti ricadute dal punto di vista ingegneristico. Proprio pensando ai risvolti applicativi, è interessante studiare tali moti per diversi modelli di fluidi non newtoniani, sotto l'influenza di un campo magnetico esterno (MHD) o in presenza di trasmissione del calore. Due modelli di fluidi considerati sono il modello micropolare e i nanofluidi. Il modello micropolare ha, rispetto a un fluido newtoniano, un descrittore in più che tiene in considerazione il moto rotatorio delle particelle del fluido.
I nanofluidi, invece, rappresentano un modello introdotto recentemente per descrivere miscele di nanoparticelle (1-100 nm) immerse in un fluido base, aventi particolari proprietà termiche.

Collaborazioni

• Michel Destrade (NUI Galway)
• Davide Riccobelli (PoliMI)
• Luca Lussardi (PoliTO)
• Giulia Bevilacqua (UniPI)
• Alessandro Giacomini (UniBS)
• Maria Cristina Patria (UniFE)
• Raimondo Penta (University of Glasgow)

Pubblicazioni di Alfredo Marzocchi

Pubblicazioni di Alessandro Musesti

Pubblicazioni di Giulia Giantesio