Geometria
L'attività del gruppo di Geometria si sviluppa essenzialmente lungo due direttrici principali: Geometria sintetica e discreta e Geometria differenziale e applicazioni. Di seguito vengono descritti separatamente i filoni di ricerca nei due ambiti.
Geometria differenziale e applicazioni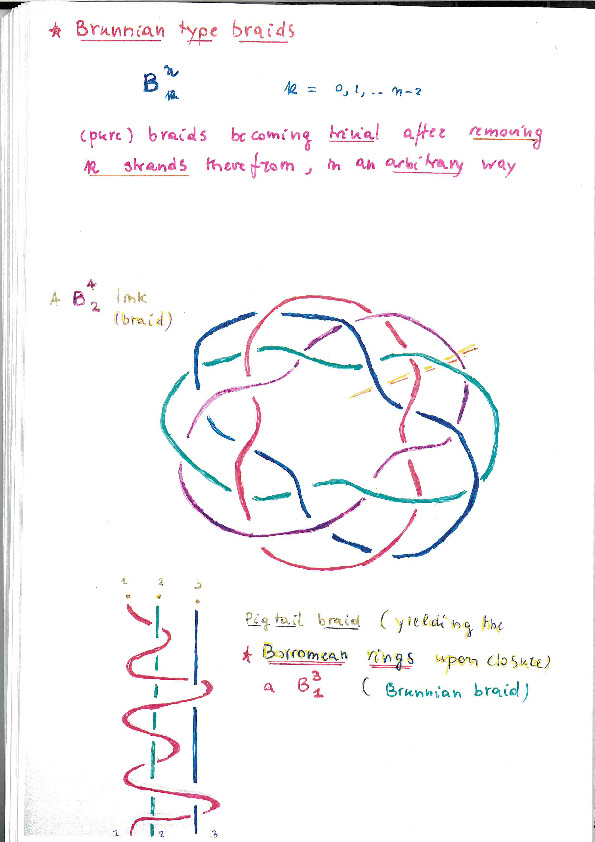
(M. Spera)
Il presente ambito si ramifica in vari percorsi tra loro collegati, descritti di seguito: l'idea soggiacente consiste nell'affrontare i vari problemi con tecniche di geometria, analisi e topologia moderne, nello spirito dell'approccio di Chern e del teorema di Atiyah-Singer. Costante è il rapporto con la fisica moderna quale fonte di problemi e principio euristico.
- Estensioni della teoria dell'indice a spazi di cappi (loop spaces). Geometria differenziale di varietà di dimensione infinita che emergono in teoria dei campi (classica e quantistica).
- Geometria simplettica e multisimplettica, quantizzazione geometrica, stati coerenti, meccanica quantistica geometrica: aspetti generali. Geometria non commutativa.
- Aspetti geometrici della teoria dei vortici. Invarianti di nodi e trecce (approccio geometrico differenziale). Spazi di nodi singolari e loro quantizzazione geometrica; descrizione semiclassica e idrodinamica di invarianti di nodi.
- Aspetti geometrici e topologici della fisica della materia condensata.
- Applicazioni della geometria riemanniana a problemi di visione computazionale.
- Aspetti matematici e storici della cartografia.
Segnaliamo anche i seguenti progetti nell'ambito del Dottorato internazionale in Science (UCSC, KU-L, ND, PUC) - Projects within the International Ph.D. Programme in Science involving Università Cattolica del Sacro Cuore (UCSC) di Milano (Brescia) - Italy, KU Leuven - Belgium, Notre Dame - USA, Pontificia Universidad de Chile - Chile:
Differential geometry and applications to modern physics
Coordinators: Mauro Spera (UCSC-Brescia) and Marco Zambon (KU Leuven)
The present project proposes some mutually intermingled research paths, mostly focussed towards symplectic geometry and its n-plectic (equivalently, multisymplectic) generalisations, together with applications to modern physics issues, both classical and quantum mechanical, with an emphasis on topological aspects.
Ph.D. Student: Antonio Michele MITI
Classical and noncommutative geometry applied to Quantum Hall Effect and other condensed matter problems
Coordinators: Giuseppe De Nittis (PUC-Santiago de Chile) and Mauro Spera (UCSC-Brescia)
The present project proposes some mutually intermingled research paths, mostly focussed towards classical and noncommutative geometry together with applications to modern physics issues, notably condensed matter physics, with an emphasis on Quantum Hall Effect (QHE) and its related topological aspects.
Ph.D. Student: Maximiliano SANDOVAL
Collaborazioni nazionali e internazionali:
Giuseppe De Nittis (PUC, Cile)
Andrea Galasso (Milano Bicocca)
Henrique Leitao (ULisboa, Portogallo)
Antonio Michele Miti (UCSC e KU Leuven, Belgio)
Maximiliano Sandoval (PUC, Cile)
Nicola Sansonetto (Università di Verona)
Tilmann Wurzbacher (Université Lorraine, Francia)
Marco Zambon (KU Leuven, Belgio)
Geometria sintetica e discreta
(S. Pianta; S. Pagani)
Fondamenti di Geometria e Algebra geometrica
I fondamenti della geometria euclidea reale secondo David Hilbert si basano com'è noto su cinque gruppi di assiomi. Se si prescinde dall'assioma di parallelismo e dal gruppo degli assiomi di continuità, si parla, in dimensione 2, di un piano assoluto (o piano di Hilbert) in cui, nel caso non archimedeo, può capitare che aspetti di tipo iperbolico coesistano con caratteristiche metriche di tipo euclideo o ellittico. Le proprietà geometriche di un piano assoluto risultano strettamente correlate alle proprietà algebriche del campo che lo coordinatizza nonché alla particolare struttura del suo gruppo di isometrie.
Noi ci occupiamo di scoprire e determinare rigorosamente tali legami, analizzando anche le diverse strutture di loop (generalizzazione non associativa di un gruppo) generate in modo naturale da sottoinsiemi regolari di isometrie.
Alcune delle tecniche di costruzione di tali loop possono essere utilizzate anche a partire da gruppi proiettivi su campi finiti, permettendoci di ottenere risultati che collegano geometria combinatoria e teoria dei gruppi e dei loop finiti.
Parallelismi in spazi proiettivi e Algebre di quaternioni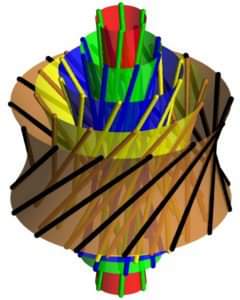
Gli spazi di rette con parallelismo (che generalizzano gli spazi affini) sono spazi lineari fra le cui rette è definita una relazione di equivalenza tale che ogni classe di equivalenza sia una partizione dell'insieme dei punti; se su di essi opera un gruppo transitivo di traslazioni si parla di strutture di traslazione (studiate da numerosi autori tra gli anni '60 e '80), la cui classificazione è legata dalla classificazione dei gruppi con partizione non banale. Una vasta classe di tali strutture, che nel caso infinito comprende anche alcuni gruppi di Lie, si può ottenere a partire da algebre quadratiche e risulta costituita da spazi immergibili in spazi proiettivi e dotati di due parallelismi. I classici parallelismi di Clifford dello spazio proiettivo tridimensionale reale ne sono l'archetipo: questi si possono descrivere utilizzando le moltiplicazioni sinistre e destre del corpo dei quaternioni di Hamilton.
Noi ci occupiamo di generalizzazioni dei parallelismi di Clifford, immergibili in spazi proiettivi e non, e a partire da campi diversi da R. Si ottengono in tal modo strutture nuove il cui studio degli automorfismi geometrici permette di gettare luce sui gruppi di automorfismi non lineari di algebre e corpi di quaternioni generalizzati. Inoltre, considerando le rappresentazioni di tali parallelismi sulla quadrica di Klein, si possono trovare interessanti legami con importanti e recenti filoni di geometria combinatoria e d'incidenza (fibrazioni di spazi proiettivi, piani di traslazione, spazi polari, flock, disegni divisibili...).
Tomografia discreta
La tomografia studia la ricostruzione di un’immagine a partire dalle sue proiezioni. In generale, si tratta di un problema mal posto a causa della presenza delle cosiddette switching component, che generano ambiguità nella ricostruzione.
Il nostro lavoro si focalizza sulle condizioni da porre per garantire unicità di ricostruzione, combinando informazioni geometriche, quali ad esempio la convessità dell’oggetto da ricostruire, con tecniche ed algoritmi propri di ambienti più applicati. Ci occupiamo inoltre della ricerca di collegamenti tra la tomografia discreta ed altri ambiti, quali la teoria dei grafi, la geometria proiettiva e la teoria dei numeri.
Collaborazioni nazionali e internazionali
Simone Costa, Luca Giuzzi, Stefano Pasotti, Elena Zizioli (Università degli Studi di Brescia)
Paolo Dulio (Politecnico di Milano)
Andrea Frosini (Università di Firenze)
Simone Rinaldi (Università di Siena)
Hans Havlicek (Technical University, Vienna)
Helmut Karzel (Technical University, Munich)
Andrea Blunck (Hamburg University)
Mahfouz Rostamzadeh (Soran University, Iraq)
Sayed Ghahreman Taherian (Isfahan University of Technology, Iran)
Robert Tijdeman (Leiden University)
Pubblicazioni di Silvia Pianta
